第3節 新古典經濟學家教你怎樣買蘋果與橘子
接著,就讓我們看看新古典經濟學家教你應該怎樣去購買蘋果與橘子,或是新古典經濟學家描述你是怎樣購買蘋果與橘子的標準理論。
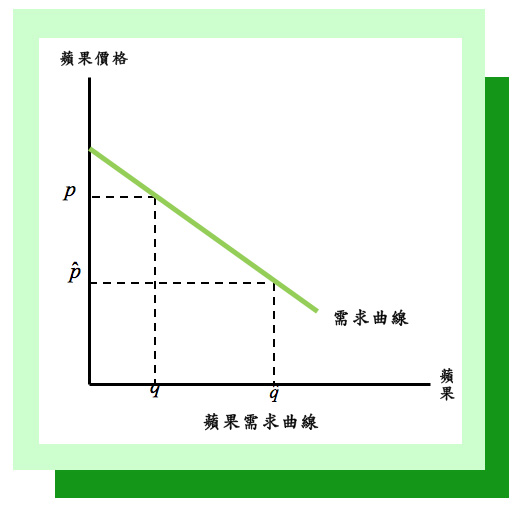
你(身上或心上)有若干元(如M元),來到一家水果行,蘋果一公斤若干元(如p元),橘子一公斤若干元(如q元)。告訴我,你會以怎樣的思維方式來決定要買幾公斤蘋果與幾公斤橘子呢?或進一步,以經濟學非常常用的分析工具─需求曲線─來說,你對蘋果與橘子的需求曲線會長什麼樣子呢?蘋果(或橘子)需求曲線的意義是指在其他條件(如所得、偏好與其他商品的價格)不變下於各種不同的蘋果(或橘子)的價格下你會買多少數量的蘋果(或橘子)的意思。以圖形來說,蘋果需求曲線是指被畫在以蘋果數量為橫軸且以蘋果(或橘子)的價格為縱軸的平面上,用來刻畫消費者在各種不同價格下會買多少數量蘋果(或橘子)的一條線。
如果你學過主流的新古典經濟學,即你的腦袋進過西洋經濟學大師所創建的經濟學思想加工廠加工過。具體而言,若你渡海讀過英美等西方國家大學的幾乎任何一個經濟學系或研究所,或若你讀過現今西方學者所寫的幾乎任何一本經濟學原理或個體經濟學的原文教科書,或你讀過台灣經濟學家模仿西方經濟學者所撰寫任何一本初級或中級經濟學教科書,或你上過台灣幾乎任何的經濟學的初級或中級課程,則幾乎百分之一百或千篇一律地,雖然你內心深處的純真知覺可能會覺得怪怪的,但是你通常會在以理智控制自己的純真潛意識之下,以違反你純真自然的意識的方式,刻意地依照主流經濟學教導你的標準作業流程,清楚地知道尋找正確答案的標準作業程序,要分成三個步驟:找出或劃出你的為數眾多的無異曲線(線上的每一點所表示的蘋果與橘子數量組合會帶給你相同的滿足水準的曲線);找出或劃出你的預算限制線;然後找出你的預算可達到的(即買得起的)且能帶給你最高效用的一條無異曲線(在蘋果與橘子的數量對你來說都是越多越好且數量是可連續微小細分等假設下),通常這條帶給你最高效用的線就是那一條與你的預算線相切的無異曲線,此時此切點所對應的蘋果與橘子的數量,就是你應該購買的最佳數量組合。
這樣的無異曲線配合預算限制線的圖形是被畫在一個以橫軸上的刻度代表蘋果的數量,縱軸上的刻度代表橘子的數量,並且以兩者的數量都是零的原點為基準點的兩度空間(或二維空間)的平面座標系中。接著,這三項標準作業程序可較詳細地說明如下:
第一步驟,怎樣畫出你的出無異曲線呢?這項任務是相當麻煩的工作。首先,無異曲線的意義是該線上的每一點所表示的蘋果與橘子數量組合會帶給消費者相同的滿足水準。一種畫出無異曲線的方法是,我們可以以平面上的任何一點作為基準點,然後(理想上或原則上)你將平面上所有點(其實是有無窮多個點)拿來與這一個任意的基準點相比較,兩個接著兩個(一次接著一次)的進行比較。將和基準點比起來一樣好(相同偏好)的所有點都歸為同一群,再將和基準點比起來更好(偏好較強)的所有的點都歸為同一群,又將和基準點比起來更不好(偏好較弱)的所有的點都歸為另一群。這時候在一些(如你來說蘋果與橘子對都是數量越多越好等)假設下,那一些和基準點比起來一樣好(相同偏好)的所有的點剛好會在平面上會呈現為一條負斜率的無異曲線。在經過這辛苦的過程後,你終於可以找到自己的第一條無異曲線了;但是這辛苦的工作才開始而已,接著你要開始在另外兩群的商品組合中再找出一個基準點,再將上述的勞苦工作重新做一次,藉此你可以找出第二條無異曲線。接著,應用同樣的方法你必須去找出你的第3、4、5、6、7…100…1000…10000000…。在經歷這般千辛萬苦的過程後,你終於找到你所有的無異曲線了。
幽默一點來說,這讓我想起李商隱的詩:「春蟬到死絲方盡,蠟炬成灰淚始乾」;關於畫無異曲線這一回事,恐怕到了絲盡蟬死且淚乾蠟炬成灰的地步,你也畫不盡你自己的無異曲線;恐怕即使物換星移地老天荒,你還是僅能像精衛填海一樣只是徒勞無功罷了。
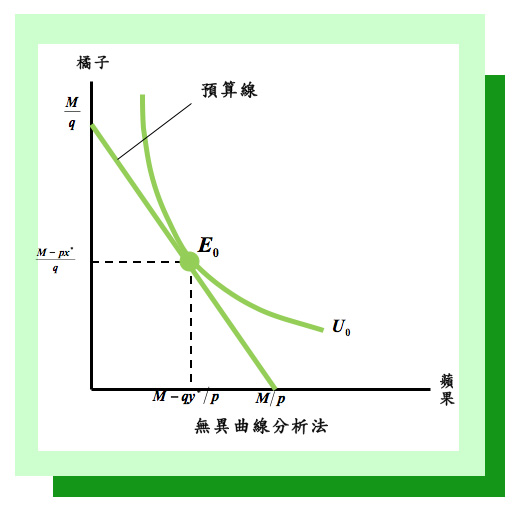
第二步驟,怎樣畫出你的預算限制線呢?這項任務(在只有兩種商品的非常單純的情況下)則是相當簡單輕鬆的工作。首先,看看若將你全部的錢(預算)用來買蘋果最多可以買幾公斤,簡單的數學告訴我們可以買M/p公斤,然後我們可以將這個數據畫在表示蘋果數量的橫軸上的相應刻度上。其次,再看看若將你全部的錢拿來買橘子最多可以買幾公斤,簡單的數學告訴我們可以買M/q公斤,然後我們可以將這個數據畫在表示橘子數量的縱軸上對應的刻度上。最後,畫一條直線連接上述橫軸與縱軸上的兩點,這一條直線就是你的預算限制線。預算限制線的斜率表示這兩種水果的相對價格或兩種水果客觀替換比率,預算限制線與垂直與水平的兩軸所構成的空間之內的所有點所表示兩種水果的組合是你的預算買得起的,此空間外的所有點是你買不起的,而預算線上的每一點則正好表示用盡你全部金錢(預算)所能購買的兩種水果的最大組合。(在有多種商品的情況下,要找出多維空間的「預算限制線」,其實也是非常困難的事。)
第三步驟,怎樣找到與一條與預算線相遇的效用最高的無異曲線(或與之相切的無異曲線)呢?這個步驟比較簡單,就直接由你的預算所達到的(即買得起的)的無異曲線中找出能帶給你最高效用的一條無異曲線,通常帶給你最高效用的無異曲線就是那一條與你的預算線相切的無異曲線,此時此切點所對應的蘋果與橘子的數量,就是你應該購買的數量組合。
由於,這兩種水果的相對價格表示兩種水果的客觀替換比率,無異曲線的斜率表示對你來說這兩種水果你主觀上願意互換的交換比率。最佳選擇會出現在兩種交換比率相同的情況上,因為若主觀與客觀交換比率不同時,透過調整購買組合就可以提高你的效用。